Dreiemoment
Dreiemoment (kraftmoment, torsjonsmoment) er i fysikken ei nemning for ei kraft si evne til å endra rotasjonen til ein lekam.
Definisjon[endre | endre wikiteksten]
Dreiemoment er definert som kraft gongar arm, der arma er kortaste avstand mellom angrepslinja til krafta og rotasjonssenteret. Symbolet (den greske bokstaven tau) vert ofte nytta for dreiemoment. SI-eininga for dreiemoment er Nm (Newtonmeter).
Til dømes gjev ei kraft på 2 Newton som verkar 5 meter frå rotasjonssenteret like stort dreiemoment som ei kraft på 10 Newton som verkar 1 meter fra rotasjonssenteret, under føresetnad om at kraft og arm står normalt (vinkelrett) på kvarandre. Formelt kan ein uttykkja dreiemoment som kryssproduktet av kraft og arm:
der F er krafta og r er avstanden mellom angrepspunktet til krafta og rotasjonssenteret. Dreiemoment er difor ein vektoriell storleik og retninga er vinkelrett på både kraft og arm.
Dreiemoment kan òg definerast som endringsrate per tid for dreieimpulsen L,
Eining[endre | endre wikiteksten]
Eininga for dreiemoment må ikkje forvekslast med eininga for arbeid som òg er Nm (som tilsvarer 1 joule). Arbeid er definert som skalarproduktet av kraft og strekning,
medan dreiemoment er definert som kryssproduktet av kraft og arm. Skilnaden ligg i at meter (m) i eininga Newtonmeter (Nm) står vinkelrett på krafta (N), medan for arbeid har strekning og kraft (m og N) samanfallande retning. Eit dreiemoment på 1 N·m påført gjennom ein heil omdreiing vil tilsvara nøyaktig 2π joule.
Dreiemoment som funksjon av tid[endre | endre wikiteksten]
Dreiemoment er den tidsderiverte av dreieimpulsen, akkurat som kraft er den tidsderiverte av fart:
der L er dreieimpulsen. Dreieimpulsen på ein stiv lekam kan uttrykkast ved tregheitsmoment I og vinkelhastigheita til lekamen:
Om I er konstant, har ein at
der α er vinkelakselerasjonen.
Døme[endre | endre wikiteksten]
Korleis er det lettast å løysa skruen?[endre | endre wikiteksten]
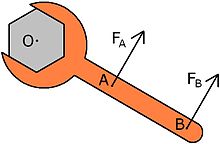
Ein ynskjer å finna ut kvar det er best å plassera krafta for å løysa ein skrue som sit godt fast, som vist i Fig. 1. Definisjonen på dreiemoment er kraft gonger arm. For å løysa skruen er det difor best å plassera krafta så langt frå rotasjonssenteret O som mogleg. Det løner seg med andre ord å plassera krafta i punkt B i staden for i punkt A. Dreiemomentet til krafta om punkt O er større enn dreiemomentet til krafta om punktet O. Mekanikarar nyttar ofte ein lang arm (om lag ein halv meter), for å løysa eller dra til skruar med stort moment. Av di ein ikkje treng så stor kraft når arma er lang vert ho kalla «latmannsarm».
Skruar, mutterar og boltar bør festast med eit bestemt moment for at delane ikkje skal losna ved vanleg belastning, og for at materialet ikkje skal verta øydelagt av at delane vert stramma for hardt. Til dette føremålet kan ein nytta ein momentnøkkel, som syner momentet ein dreg til med på ein skala, eller han kan gje etter ved eit moment som er innstilt på førehand. Eit typisk døme på bruk av momentnøkkel er for å trekkja til skruane som festar topplokket på motorar.
Sjå òg[endre | endre wikiteksten]
Kjelder[endre | endre wikiteksten]
- Denne artikkelen bygger på «Dreiemoment» frå Wikipedia på bokmål, den 8. april 2008.










