Flatetregleiksmoment

Flatetregleiksmoment, eller anna flatemoment, er ein storleik som gjev eit mål for korleis ei geometrisk flate fordeler seg om ei linje i flata.

Kvar enkelt flatedel blir multiplisert med kvadratet av avstanden sin, y, frå linja, og summen av alle desse produkta er lik flata sitt flatetregleiksmoment med omsyn på den valde linja.

I=\int \limits _{A}y^{2}\,dA

Om ein reknar ut flatetregleiksmomentet om ei linje normalt på flata, vert det kalla polart flatetregleiksmoment .

Omgrepet har særs stor tyding mellom anna i teorien for bøying av bjelkar, ved torsjon og i statikk.

Rektangulært tverrsnitt[endre | endre wikiteksten]

Steinerteoremet for utrekning anna arealmoment

Integralet vert løyst på følgjande måte på måte for eit rektangulært tverrsnitt:

I_{x}=\int \limits _{-h/2}^{h/2}y^{2}\,bdy={\left[{\frac {y^{3}b}{3}}\right]}_{-h/2}^{h/2}={\frac {bh^{3}}{12}}

der h er høgda, og b er breidda av det rektangulære tverrsnittet. I_x blir da flatetregleiksmomentet om x-aksen i senteret C.

Sirkulært tverrsnitt[endre | endre wikiteksten]

Integralet er ikkje vist her, men eit røyrtverrsnitt vert rekna ut frå $I={\frac {\pi D^{4}}{64}}$ , der D er ytterdiameteren.

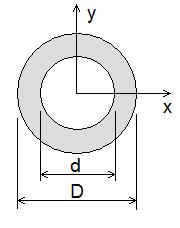
Røyrtverrsnitt[endre | endre wikiteksten]

$I={\frac {\pi }{64}}(D^{4}-d^{4})$

der D er ytterdiameteren, og d er innerdiameteren.

Bruk av flatetregleiksmoment[endre | endre wikiteksten]

Eit vanleg bruksområde av flatetregleiksmoment er ved utrekning av bøyespenninga, $\sigma _{b}$ i ein bjelke.

$\sigma _{b}={\frac {M}{I}}y$

der M er momentet, I er flatetregleiksmomentet og y er avstanden frå arealsenteret til punktet der du ønsker å rekne ut spenninga. Dersom du har eit rektangulært tverrsnitt er y = h/2.

Steinerteoremet[endre | endre wikiteksten]

Dersom du har eit tverrsnitt som er samansett av fleire areal som ikkje ligg på same akse som tyngdepunktet av arealet, er det vanleg å bruke Steinerteoremet for å rekne ut flatetregleiksmomentet, kalla parallellakseteoremet, eller Steinersatsen.

$I_{z}=I_{x}+Ad^{2}.\,$ , der I_x er flatetregleiksmoment for arealet som ligg på ein parallell akse utanfor arealsenteret (i akse z), d er avstanden frå arealsenteret i akse z til arealsenteret av A.

Motstandsmomentet[endre | endre wikiteksten]

Eit anna vanleg omgrep i bjelkeberekningar er motstandsmomentet eller tverrsnittsmodulen (engelsk section modulus), og vert ofte skrive W. I vanleg praksis vert bøyespenningen $\sigma _{b}$ rekna ut frå

\sigma _{b}={\frac {M}{W}}

, der

W={\frac {I}{y}}={\frac {I}{h/2}}

siden arealsenteret til tverrsnittet vanlegvis ligg i midten av tverrsnittet, og følgjeleg er avstanden frå senteret av tverrsnittet til ytste fiber lik h/2.

Motstandsmomentet for nokre vanlege tverrsnitt er gjeve under