Linearisering

Linearisering er ein metode i matematikk for å finne ei lineær tilnærming til ein funksjon ved eit visst punkt. I studiet av dynamiske system er linearisering ein metode for å undersøke stabiliteten til eit likevektspunkt i eit system av ikkje-lineære differensiallikningar eller diskrete dynamiske system.. Denne metoden vert nytta i felt som ingeniørvitskap, fysikk, økonomi og økologi.

Linearisering av ein funksjon

Lineariseringar av ein ein funksjon er linjer som ein vanlegvis nyttar for utrekning. Linearisering er ein effektiv metode for å tilnærme resultatet av ein funksjon $y = f(x)$ ved alle $x = a$ basert på verdien og hellinga til funksjonen ved $x = b$, om f(x) er kontinuerleg på $[a, b]$ (eller $[b, a]$) og at $a$ er nær $b$. Kort sagt, linariseringa tilnærmar resultatet til ein funksjon nær $x = a$.

Til dømes veit du kanskje at $\sqrt{4} = 2$. Men utan ein kalkulator, kva vil vere ei god tilnærming av $\sqrt{4.001} = \sqrt{4 + .001}$?

For alle funksjonar $y = f(x)$, kan $f(x)$ tilnærmast om han ligg nær eit kjend kontinuerleg punkt. Det mest grunnleggande kravet er at der $L_a(x)$ er lineariseringa av f(x) at x = a er $L(a) = f(a)$. Punkt-hellings-forma av ei likning dannar ei likning for ei linje, om ein har punktet $(H, K)$ og hellinga $M$. Den generelle forma for denne likninga er: $y - K = M(x - H)$.

Ved å nytte punktet $(a, f(a))$, vert $L_a(x)$ til $y = f(a) + M(x - a)$. Fordi kontinuerlege funksjonar er lokalt lineære, er den beste hellinga å erstatte hellinga til linjetangenten til $f(x)$ ved $x = a$.

Sidan lokal linearitet gjeld for dei fleste punkta vilkårleg nær til $x = a$, vil dei som ligg relativt nær fungere bra for lineære tilnærmingar. Trass alt bør hellinga $M$ vere i det mest nøyaktige tilfellet lik hellinga til tangentlinja ved $x = a$.

Ei tilnærming av f(x) ved (x, f(x))

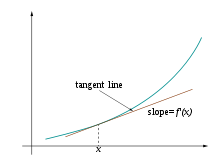
Visuelt syner figuren tangentlinja til $f(x)$ ved x. Ved $f(x+h)$, der $h$ er ein liten positiv eller negativ verdi, er f(x+h) særs nær verdien til tangentlinja i punktet $(x+h, L(x+h))$.

Den siste likninga for lineariseringa av ein funksjon ved $x = a$ er:

$y = f(a) + f'(a)(x - a)\,$

For $x = a$ er $f(a) = f(x)$. Den deriverte til $f(x)$ er $f'(x)$ og hellinga til $f(x)$ ved $a$ er $f'(a)$.

Døme

For å finne $\sqrt{4.001}$ kan vi nytte det vi veit, $\sqrt{4} = 2$. Lineariseringa til $f(x) = \sqrt{x}$ ved $x = a$ er $y = \sqrt{a} + \frac{1}{2 \sqrt{a}}(x - a)$, sidan funksjonen $f'(x) = \frac{1}{2 \sqrt{x}}$ definerer hellinga til funksjonen $f(x) = \sqrt{x}$ ved $x$. Ved å setje inn $a = 4$, vert lineariseringa til 4 $y = 2 + \frac{x-4}{4}$. I dette tilfellet er $x = 4.001$, så $\sqrt{4.001}$ er tilnærma $2 + \frac{4.001-4}{4} = 2.00025$. Den verkelege verdien er nær 2.00024998, så lineariseringa har ein relativ feil på mindre enn ein milliondel av ein prosent.

Linearisering av ein multivariabel funksjon

Likninga for lineariseringa av ein funksjon $f(x,y)$ i eit punkt $p(a,b)$ er:

$f(x,y) \approx f(a,b) + \left. {\frac{{\partial f(x,y)}}{{\partial x}}} \right|_{a,b} (x - a) + \left. {\frac{{\partial f(x,y)}}{{\partial y}}} \right|_{a,b} (y - b)$

Den generelle likninga for lineariseringa av ein multivariabel funksjon $f(\mathbf{x})$ i eit punkt $\mathbf{p}$ er:

$f({\mathbf{x}}) \approx f({\mathbf{p}}) + \left. {\nabla f} \right|_{\mathbf{p}} \cdot ({\mathbf{x}} - {\mathbf{p}})$

der $\mathbf{x}$ er vektoren av variablar og $\mathbf{p}$ er lineariseringa til punktet ein undersøker..

Bruk av linearisering

Linearisering gjer det mogeleg å nytte metodar for å studere lineære system til å analysere korleis ikkje-lineære funksjonar oppfører seg nær eit visst punkt. Lineariseringa til ein funksjon er det førsteordens leddet til taylorutvidinga rundt punktet ein undersøker. For eit system definert av likninga

$\frac{d\bold{x}}{dt} = \bold{F}(\bold{x},t)$,

kan det lineariserte systemet skrivast

$\frac{d\bold{x}}{dt} = D\bold{F}(\bold{x_0},t) \cdot (\bold{x} - \bold{x_0})$

der $\bold{x_0}$ er punktet ein undersøker og $D\bold{F}(\bold{x_0})$ er den jacobiske til $\bold{F}(\bold{x})$ ved $\bold{x_0}$.

Stabilitetsanalyse

I stabilitetsanalyse kan ein nytte eigenverdiane til jacobimatrisa i eit likevektspunkt for å avgjere eigenskapane til likevekta. Om alle eigenverdiane er positive er likevekta ustabil og om alle er negative er likevekta stabil. Om verdiane er både positive og negative er likevekta eit sadelpunkt. Alle komplekse eigenverdiar vil dukke opp i kompleks-konjugerte par og indikere ein spiral.

Sjå òg

• Stabilitetsderivat
• Lineariseringsteorem
• Taylortilnærming

Kjelder

• Denne artikkelen bygger på «Linearization» frå Wikipedia på engelsk, den 10. mars 2010.
  • Wikipedia på engelsk oppgav desse kjeldene: