Integral
Eit integral av ein matematisk funksjon er i differensialrekning ei utviding av konseptet summasjon. Prosessen med å finne integral vert kalla integrasjon eller integrering, og vert vanlegvis brukt for å finne totalsummen av eigenskapar som areal, volum, masse, forskyving osv, når fordelinga eller endringsraten med omsyn til andre storleikar (posisjon, tid) er spesifisert. Det finst fleire forskjellige definisjonar på integrasjon som inneber forskjellige tekniske metodar. Dei er derimot samsvarande, og to forskjellige måtar å integrere ein funksjon på vil gje same resultat når begge er definert.
Uttrykket «integral» kan òg referere til antideriverte. Sjølv om dei er nært knytt saman gjennom analysen sitt fundamentalteorem, er dei to førestillingane omgrepsmessig forskjellige. Ein antiderivert vert ofte referert til som eit ubestemt integral (ein funksjon), medan integral i denne artikkelen omhandlar bestemte integral.
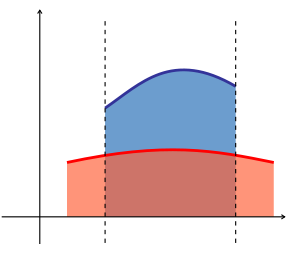
Integralet til ein funksjon f med ein reell variabel x på intervallet [a, b] er lik arealet mellom linjene x = a, x = b, x-aksen, og kurva som vert definert av grafen til f. Dette vert formalistert av den enklaste forma av eit integral, Riemann-integralet, som gjev oss ein metode for å rekne ut dette arealet ved å bruke grenser for å dele arealet inn i tynnare rektangulære striper og føreta summen av arealet til kvar stripe. (sjå døme på dette).
Eit alternativ er å la
slik at integralet av f mellom a og b er eit mål av S. I denne metoden gjev integrasjon eit tal knytt til S, som gjev oss ein ide om «storleiken» til settet (men dette er forskjellig frå kardinalitet eller storleiksorden). Dette fører til ein annan og meir mektig definisjon av integralet, kalla Lebesgue-integral.
Leibniz introduserte lang s som notasjon for integralet. Integralet diskutert over ville då ha vore skrive . -teiknet representerer integrasjonen, a og b er grenseverdiane i intervallet, f(x)' er funksjonen som vert integrert, kalla integrand, og dx er notasjonen for integrasjonsvariabelen. Historisk sett representerte dx ein infinitesimal storleik, og lang s stod for «sum». I moderne integrasjonsteoriar, som er bygd opp på andre grunnlag, vert ikkje denne notasjonen lenger tenkt på som ein sum, bortsett frå i dei mest uformelle tilfella. I dag representerer dx eit differensial.
Viss f til dømes er ein konstant funksjon f(x) = 3, så vil integralet av f mellom 0 og 10 vere arealet av rektangelet som er avgrensa av linjene x = 0, x = 10, y = 0, og y = 3. Arealet til dette rektangelet er breidda multiplisert med høgda, så verdien av integralet er 30. Det same resultatet vil ein finne ved å integrere funksjonen, men metoden vert vanlegvis brukt for meir kompliserte eller glatte kurver.
Rekne ut integral
[endre | endre wikiteksten]Den mest grunnleggande teknikken for å rekne ut integral med ein reell variabel er basert på analysen sitt fundamentalteorem. Det føregår slik:
- Vel ein funksjon f(x) og eit intervall [a, b].
- Finn ein antiderivert av f, altså ein funksjon F slik at F' = f.
- Fundamentalteoremet gjev, så lenge integranden og integralet ikkje har singularitetar på integrasjonsvegen, at
- Derfor er verdien av integralet F(b) − F(a).
Merk at integralet ikkje eigentleg er den antideriverte, men fundamentalteoremet tillet oss å bruk antideriverte til å utrede bestemte integral.
Det vanskelege er ofte å finne ein antiderivert av f. Det er sjeldan mogeleg å ta ein kikk på ein funksjon og skrive ned den antideriverte. Ofte er det nødvendig å bruke ein av dei mange teknikkane som er utvikla for å rekne ut integral. Dei fleste av desse teknikkane går ut på å skrive om eit integral til eit anna integral, som kanskje er lettare å finna antideriverte til. Desse teknikkane er mellom anna:
- Integrasjon ved innsetjing
- Delvis integrasjon
- Trigonometrisk erstatning i integrasjon
- Partialbrøk i integrasjon
Sjølv om ingen av desse teknikkane skulle føre fram, er det framleis mogeleg å evaluere eit gjeve integral. Ein annan teknikk som er ganske vanleg er restanalyse, der Taylor-rekkjer av og til kan brukast for å finne antideriverte. Det finst òg fleire andre måtar å rekne ut bestemte integral på, til dømes kan Parsevals identitet brukast til å transformere eit integral over eit rektangulært område til ein uendeleg sum. Av og til må ein gjere eit triks for å rekne ut eit integral. For døme på dette sjå gaussisk integral.
Tilnærming av bestemte integral
[endre | endre wikiteksten]Bestemte integral kan tilnærmast ved å bruke fleire metodar av numerisk integrasjon. Ein populær metode, kalla rektangelmetoden, går ut på å dele området under funksjonen opp i ei rekkje rektanglar, og så finne summen av desse. Andre metodar er trapesregelen og Simpsons regel.
Enkelte integral kan ein ikkje finne eksakt, medan andre integral er så kompliserte at ein om ein skulle finne eit eksakt svar så ville det teke svært lang tid med mykje utrekning. Ei tilnærming er derimot ein proesess som byggjer på innsetjing, multiplisering, addisjon og dividering av variablar. Dette kan lett gjerast med moderne kalkulatorar og datamaskinar. Mange problemstillingar i den verkelege verda er avhengig av å kunne rekne ut tilnærma verdiar av intregral, fordi formlane elles ville vore svært kompliserte, og fordi ein ofte ikkje treng eit heilt eksakt svar.
Uekte integral
[endre | endre wikiteksten]Ikkje alle integral kan reknast ut ved å bruke ein enkel grenseprosess. Eit integral som berre kan reknast ut ved å sjå på det som grensa av integral for større og større intervall vert kalla uekte integral. Uekte integral får ein vanlegvis når rekkevidda til funksjonen som skal integrerast er uendeleg, eller i tilfellet med Riemann-integral, når domenet til funksjonen er uendeleg. Eit døme på eit uekte integral er Cauchy sin pålydande verdi.
Forskjellige integral
[endre | endre wikiteksten]Dei viktigaste integrala er Riemann-integralet og Lebesgue-integralet. Riemann-integralet vart utvikla av Bernhard Riemann i 1854 og var den første klåre definisjonen av integralet. Lebesgue-integralet vart utvikla av Henri Lebesgue for å integrere fleire typar funksjonar og for å gje eit teorem om utvekslande grenser og integral.
Sjølv om Riemann- og Lebesgue-integrala er dei viktigaste, har ein fleire andre integral som:
- Daniell-integral.
- Darboux-integral, ein variant av Riemann-integralet.
- Denjoy-integral (òg kalla Henstock-Kurzweil-integral), ei utviding av både Riemann- og Lebesgue-integrala.
- Haar-integral.
- Henstock-Kurzweil-Stieltjes-integral (òg kalla HK-Stieltjes-integral).
- Lebesgue-Stieltjes-integral (òg kalla Lebesgue-Radon-integral).
- Perron-integral, som tilsvarar det avgrensa Denjoy-integralet.
- Riemann-Stieltjes-integral, ei utviding av Riemann-integralet.
Definisjonar ved hjelp av integral
[endre | endre wikiteksten]Fleire matematiske funksjonar og konstantar kan definerast ved å bruke eit integral. Den naturlege logaritmen, skriven ln(x), er definert for alle x > 0 som
Derfor kan den matematiske konstanten e definerast som det unike talet som oppfyller
Både betafunksjonen og gammafunksjonen er definert i form av integral.
Notasjon
[endre | endre wikiteksten]Isaac Newton brukte ein liten vertikal strek over ein variabel for å indikere integrasjon, eller plasserte variabelen inni ein boks. Den vertikale streken kunne derimot lett forvekslast med eller , som Newton brukte for å indikere differensial, og boksnotasjon var vanskeleg for boktrykkarar å framstille, så desse notasjonane vart ikkje mykje brukt.
Den moderne notasjonen for eit ubestemt integral vart introdusert av Gottfried Leibniz i 1675. Han brukte integralsymbolet «∫» frå ein utstrekt S, som stod for summa (latinsk for sum). Den moderne notasjonen for det bestemte integralet, med grenser over og under integralteiknet, vart først brukt av Joseph Fourier i 1822.[1]
Kjelder
[endre | endre wikiteksten]- ↑ Tidleg bruk av symbol i differensialrekning, arkivert frå originalen 5. desember 1998, henta 22. januar 2007
Bakgrunnsstoff
[endre | endre wikiteksten]- Funksjonskalkulator av Wolfram Research
- Funksjonskalkulator av WIMS
- P.S. Wang, Teknikkar for å løyse bestemte integral (1972)








