Fourierrekkje
Ei fourierrekkje er i matematikk ei dekomponering av ein periodisk funksjon eller eit periodisk signal til ein sum av enkle svingande funksjonar, nemleg sinus- og cosinusbølgjer (eller komplekse eksponential). Studiet av fourierrekkjer er ei grein innan fourieranalyse. Fourierrekkjer vart innført av Joseph Fourier (1768–1830) for å kunne løyse varmelikninga på ei metallplate.
Varmelikninga er ei partiell differensiallikning. Før Fourier arbeidde med dette fanst det inga kjend løysing på varmelikninga i ein generell situasjon, sjølv om nokre løysingar var kjend når varmekjelda oppførte seg på ein enkel måte, særleg om varmekjelda var ei sinus- eller cosinusbølgje. Desse enkle løysingane vert i dag stundom kalla eigenløysingar. Ideen til Fourier var å modellere ei komplisert varmekjelde som ei superposisjonering (eller ein lineær kombinasjon) av enkle sinus- og cosinusbølgjer, og så skrive løysinga som ei superposisjonering av dei tilhøyrande eigenløysingane. Denne superposisjoneringa eller lineære kombinasjonen vert kalla fourierrekkjer.
Frå eit moderne synspunkt er resultata til Fourier noko uformelle og manglar ein presis notasjon av funksjon og integral tidleg på 1800-talet. Seinare uttrykte Dirichlet og Riemann resultata til Fourier med større presisjon og formalitet.
Sjølv om den opphavlege motivasjonen var å løyse varmelikninga, vart det seinare klart at den same teknikken kunne nyttast på mange matematiske og fysiske problem. Dei grunnleggjande resultata er veldig lette å forstå ved hjelp av moderne teori.
Fourierrekkjer vert nytta innan mange felt i elektroteknikk, vibrasjonsanalyse, akustikk, optikk, signalhandsaming, biletprosessering, kvantemekanikk og mange fleire.
Definisjon[endre | endre wikiteksten]
I denne bolken er ƒ(x) ein funksjon med ein reell variabel x. Denne funksjonen vert vanlegvis rekna å vere periodisk med ein periode på 2π, som tyder at ƒ(x + 2π) = ƒ(x), for alle reelle x. Vi skal prøve å skrive ien slik funksjon som ein uendeleg sum eller ei rekkje av enklare 2π–periodiske funksjonar. Vi startar med å nytte ein uendeleg sum av sinus- og cosinusfunksjonar på intervallet [−π, π], slik Fourier gjorde, og så diskutere forskjellige formuleringar og generaliseringar.
Fourier sin formel for 2π-periodiske funksjonar ved hjelp av sinus og cosinus[endre | endre wikiteksten]
For ein 2π-periodisk funksjon ƒ(x) som er integrerbar på [−π, π], vert tala
og
kalla fourierkoeffisientane til ƒ. Ein innfører partielle summar av fourierrekkjer for ƒ, ofte skriven som
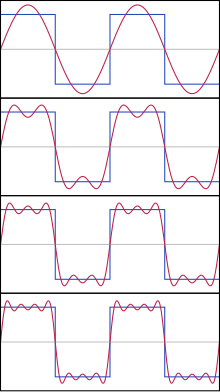
Dei partielle summane for ƒ er trigonometriske polynom. Ein ventar at funksjonane SN ƒ er tilnærma funksjonen ƒ, og at tilnærminga vert betre når N går mot uendeleg. Den endelege summen
vert kalla fourierrekkja til ƒ.
Fourierrekkjer konvergerer ikkje alltid, og sjølv når dei konvergerer for ein spesiell verdi av x0 av x, så kan summen av rekkjene ved x0 vere forskjellig frå verdien til ƒ(x0) av funksjonen. Dette er eit av hovudproblemstillingane innan harmonisk analyse for å avgjere når ei fourierrekkje konvergerer, og når summen er lik den originale funksjonen. Om ein funksjon er integrerbar på intervallet [−π, π], så konvergerer fourierrekkjene til funksjonen i nesten kvart punkt. I tekniske applikasjonar tenkjer ein seg generelt at fourierrekkjene konvergerer overalt bortsett frå i diskontinuitetar, sidan funksjonane nytta innan teknikk oppfører seg annleis enn dei funksjonane matematikarane kan nytte som motdøme til denne tanken. Særleg konvergerer fourierrekkjene absolutt og uniformt til ƒ(x) når den deriverte av ƒ(x) (som ikkje treng å eksistere overalt) er kvadratintegrerbar.[1]
Døme på ei enkel fourierrekkje[endre | endre wikiteksten]


Vi nyttar no formelen over for utvide ei fourierrekkje av ein særs enkel funksjon. Vi tar ei sagtannbølgje
I dette tilfellet er fourierkoeffisientane
Det kan visast at fourierrekkjene konvergerer til ƒ(x) i kvart punkt x der ƒ kan deriveast, og derfor:
Når x = π, fourierrekkjene konvergerer til 0, som er halvesummen av venstre- og høgregrensa til ƒ ved x = π.
Ein merkar seg at utvidinga av fourierrekkjene til funksjonen vår ser mykje mindre enkel ut enn formelen ƒ(x) = x, så det ser kanskje ikkje heilt klårt ut kvifor ein treng denne fourierrekkja. Det finst mange bruksområde for denne rekkja, og eit av dei er varmelikninga som Fourier ønskte å løyse. Tenke ei metallplate forma som ein firkant der sidene måler π meter, med koordinatar (x, y) ∈ [0, π] × [0, π]. Om det ikkje finst ei varmekjelde inne i plata, og om tre av dei fire sidene har ein temperatur på 0 °C, medan den fjerde sida, gjeven som y = π, har ein temperatur opprettheldt av temperaturgradienten T(x, π) = x grader Celsius, for x i (0, π), så kan ein vise at den stasjonære varmefordelinga (eller varmefordelinga etter at det har gått ei lang tid) er gjeven som
Her er sinh ein hyperbolsk sinus-funksjon. Denne løysinga til varmelikninga får ein ved å multiplisere kvart ledd av Li.1 med sinh(ny)/sinh(nπ). Medan dømet med funksjonen f(x) ser ut til å ha unaudsame kompliserte fourierrekkjer, så er varmefordelinga T(x, y) ikkje-triviell. Funksjonen T kan ikkje skrivast som eit lukka uttrykk. Denne metoden for å løyse varmeproblemet på kunne berre gjerast ved hjelp av metoden til Fourier.
Eit anna bruksområde for denne fourierrekkje var å løyse Basel-problemet ved hjelp av Parseval-teoremet.
Kjelder[endre | endre wikiteksten]
- Denne artikkelen bygger på «Fourier series» frå Wikipedia på engelsk, den 2. desember 2009.
- Wikipedia på engelsk oppgav desse kjeldene:
- William E. Boyce and Richard C. DiPrima, Elementary Differential Equations and Boundary Value Problems, Eighth edition. John Wiley & Sons, Inc., New Jersey, 2005. ISBN 0-471-43338-1
- Joseph Fourier, translated by Alexander Freeman (published 1822, translated 1878, re-released 2003). The Analytical Theory of Heat. Dover Publications. ISBN 0-486-49531-0. 2003 unabridged republication of the 1878 English translation by Alexander Freeman of Fourier's work Théorie Analytique de la Chaleur, originally published in 1822.
- Katznelson, Yitzhak (1976), An introduction to harmonic analysis (andre retta utg.), New York: Dover Publications, Inc, ISBN 0-486-63331-4
- Felix Klein, Development of mathematics in the 19th century. Mathsci Press Brookline, Mass, 1979. Translated by M. Ackerman from Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert, Springer, Berlin, 1928.
- Walter Rudin, Principles of mathematical analysis, Third edition. McGraw-Hill, Inc., New York, 1976. ISBN 0-07-054235-X
- ↑ Georgi P. Tolstov (1976). Fourier Series. Courier-Dover. ISBN 0486633179.
Bakgrunnsstoff[endre | endre wikiteksten]
- Ein interaktiv opplæring i fourierrekkjer Arkivert 2014-07-15 ved Wayback Machine.
- Java-applikasjon som viser fourierrekkjeutviding av ein vilkårleg funksjon
- Døme på problemstillingar Arkivert 2008-04-10 ved Wayback Machine.
- Weisstein, Eric W., «Fourier Series» frå MathWorld.



![{\displaystyle (S_{N}f)(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{N}\,[a_{n}\cos(nx)+b_{n}\sin(nx)],\quad N\geq 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cff74f4cc63376278745fc298c28130ff8939164)
![{\displaystyle {\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\,[a_{n}\cos(nx)+b_{n}\sin(nx)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a48744c1b526b072c67a1cd69300f9cebc58f5b3)



![{\displaystyle {\begin{aligned}f(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\&=2\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbf {Z} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df331d3a65b3f8e9b23673e8c41ed3e215d1ae4a)
