Vinkel

Ein vinkel er ein geometrisk figur som er danna av to rette linjer frå same punkt. Dette punktet vert kalla toppunktet til vinkelen, og linjene vert kalla beina til vinkelen. Vinkel blir brukt som eit mål på skilnaden av hellinga av dei to linjene, utan eigenleg å finne eller avgjere hellinga på kvar av linjene.
Ein kan fordjupe seg i teoriane til vinklane og bruken av dei i geometrien og i trigonometri.
Måleiningar
[endre | endre wikiteksten]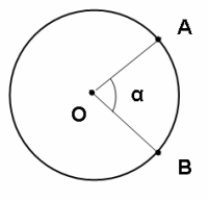
For å måle vinkelen α, den bua kurven med senter i spissen (O) av dei to linjestykka (OA og OB), brukar vi formelen:
Der k er ein konstant, s er lengda av den bua kurven (AB), delt på radiusen til sirkelen som blir brukt (OA).
Radianar
[endre | endre wikiteksten]Radianar (forkorta rad), òg kalla absolutt vinkelmål. Her er konstanten k = 1, og éin heil sirkel er avgjort til å vere 2π radianar. Dette er SI-eininga til systemet for vinkelmål.
Gradar
[endre | endre wikiteksten]Gradar (forkorta °), der éin heil sirkel er avgjort til å vere 360°. Her er konstanten k = 360/2π = 180/π.
Ei grad kan delast inn i 60 minutt (′), og eitt minutt kan delast inn i 60 sekund (″). For å skilje mellom vinkelmåla og tidseiningane nyttar ein ofte prefikset «boge-», slik at vinkelmåla blir bogeminutt og bogesekund.
Gradianar
[endre | endre wikiteksten]Gradianar (forkorta grad eller gon eller g), blir òg nokre gonger kalla nygradar, er eit nyare vinkelmål der éin full sirkel er avgjort til å vere 400 gradar. Dette gjev konstanten k = 400/2π = 200/π.
Timar
[endre | endre wikiteksten]Ei inndeling av sirkelen i 24 timar vert gjort i astronomien når vinkelen som blir målt er på himmelen og går langs ein boge som er parallell med himmelekvator. Koordinatane timevinkel og rektascensjon oppgjevast i timar, minutt og sekund, og er vinklar målt i tilhøve til ulike haldepunkt. Ein time tilsvarar 15° og 1° tilsvarar 4 minutt. Desse minutta og sekunda må ikkje forvekslast med bogeminutt og bogesekund, som er brøkdelar av éi grad.
Koplinga mellom tid og vinkel kjem av at timevinkelen til sola tilsvarar tida som er gått sidan ho sist stod i sør.
Ulike vinkeltypar
[endre | endre wikiteksten]- Ein vinkel som er mindre enn 90° blir kalla ein spiss vinkel.
- Ein vinkel som er større enn 90° blir kalla ein stump eller butt vinkel.
- Ein vinkel på 90° blir kalla ein rett vinkel. Sjå òg ortogonalitet, som tyder «rettvinkla».
 |
 |
 |
 |
- To vinklar som til saman utgjer 90°, blir kalla komplementvinklar.
- To vinklar som til saman utgjer 180°, blir kalla supplementvinklar.
- To vinklar som til saman utgjer 360°, blir kalla eksplementvinklar.
Ein formell definsjon
[endre | endre wikiteksten]Ein vinkel kan finnast ved ein rettvinkla trekant. Om ein let vere ein vinkel, og så nyttar trigonometriske funksjonar finn vi
og
for to tal x og y. Så ein vinkel i det euklidske planet kan verte gjeven av to tal x og y.
Forholdet y/x der samsvarar til to vinklar i det geometriske området 0 < θ < 2π, sidan
Om ein tillèt uendelegheit for forholdet y/x kan ein definere vinkelen θ som ein funksjon av x og y ved å nytte den inverse tangentfunksjonen for alle punkt utanom origio, om ein tenkjer at den inverse tangenten varierer frå -π/2 to π/2,
Resultatet vil varierer frå -π to π. Verdiane av x og y avgjer kva kvadrant vinkelen ligg i. Alternativt kan ein nytte den inverse cosinusfunksjonen om ein tenkjer seg at resultatet for den inverse cosinusen varierer frå 0 til π,
I dette tilfellet vil resultatet varierer frå 0 til 2π.
Kjelder
[endre | endre wikiteksten]- Delar av denne artikkelen bygger på «Vinkel» frå Wikipedia på bokmål, den 13. september 2011.
- Delar av denne artikkelen bygger på «Angle» frå Wikipedia på engelsk, den 13. september 2011.








![{\displaystyle \theta (x,y)={\begin{cases}cos^{-1}[x/r(x,y)]&y\geq 0\\2\pi -cos^{-1}[x/r(x,y)]&y<0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06009e902c82b00e3937dbabdec3e764747ec20b)