Polarkoordinatsystem
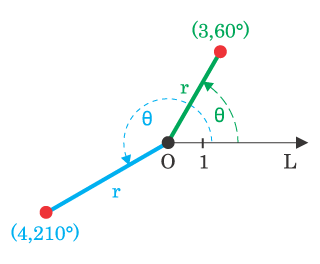
Eit polarkoordinatsystem er eit koordinatsystem der kvart punkt i eit plan er avgjort ut ifrå avstanden frå eit gjeve punkt (vanlegvis origo) og vinkel i tilhøve til x-aksen. I eit vanleg kartesisk koordinatsystem blir punkta avgjort ut ifrå avstanden til kvar koordinatakse.
Prinsippet i polarkoordinatar er at ein angjev alle punkt ved hjelp av følgjande informasjon:
- Punktet sin vinkel (gradar eller radianar ) i tilhøve til kva ein ville kalle x-aksen i eit rektangulært koordinatsystem, θ.
- Punktet sin avstand frå origo, r.
Konvertering mellom polare og kartesiske koordinatar[endre | endre wikiteksten]

Omrekning av polarkoordinatar til kartesiske koordinatar kan gjerast ved:
Medan omrekninga frå kartesiske koordinatar til polarkoordinatar kan gjerast ved:
- (gjeven ved Pythagoras’ læresetning), og
Alle desse formlene føreset at referansepunktet for polarkoordinatsystemet er origo. Arcsinfunksjonen er den inverse funksjonen til sinusfunksjonen og gjev ei løysing i intervallet [−π/2,+π/2], så formelen for θ vil gje ei løysing i intervallet [−π/2,+π/2]. Dersom ein vil finne θ i intervallet [0, 2π) kan ein òg bruke:
Bruk av polarkoordinatar[endre | endre wikiteksten]

Ei likning uttrykt i polarkoordinatar er kjent som ei polar likning. Normalt er desse likningane gjevne ved å definere r som ein funksjon av θ. Denne definisjonen gjev visse fordeler i bruken av polarkoordinatar i tilhøve til kva ein kan oppnå med rektangulære. Særleg fordelaktig er det å bruke polarkoordinatar der det inngår noko sirkulært. Det enklaste tenkjelege dømet er å framstille ein sirkel. Her er definisjonen av ein sirkel med radius 1.
Lengda til det rørlege punktet vert altså sett til konstant å vere lik éin, som altså er avstanden frå origo til periferien. Deretter blir sett vinkelen til å variere mellom dei 0 og 2π eksklusiv (eller 0 og 360° i vinklar), der heile sirkelen er med.
Arkimedisk spiral[endre | endre wikiteksten]

Ein arkimedisk spiral er ein spiral som vart oppdaga av Arkimedes, som kan forklarast med polarkoordinatar. Spiralen har formelen
Ved å forandre a vil spiralen skifte form, medan b er distansen mellom kurvene, som for ein gjeven spiral alltid er konstant. Den arkimediske spiralen har to kurver, ein for θ > 0 og ein for θ < 0. Dei to kurvene startar i origo. Sett bort frå kjeglesnitta var denne kurven av dei første til å bli skildra. Kurva er òg eit godt døme på kurver som blir best skildra med polarkoordinater.
Polar rose[endre | endre wikiteksten]

Ei polar rose er ei matematisk kurve som ser ut som ein blome med kronblad og kan defineres som ei enkel polar likning:
For ein kvar konstant (inkludert 0). Dersom k er eit heiltal vil desse likningane gje kurver der «blomen» har k kronblad når k er eit oddetal og 2k kronblad når k er eit partal. Dersom k er eit rasjonalt tal, men ikkje eit heiltal vil ein òg få fram ein blome der kronblada overlappar kvarandre. Her må derimot definisjonsintervallet for kurva vere større enn [0, 2π) for at «blomen» skal bli komplett. Merk at det er umogeleg å definere ei kurve der ein får , der n er eit heiltal, kronblad.
Variabelen a gjev lengda på kronblada.
Kjeglesnitt[endre | endre wikiteksten]
Alle kjeglesnitta kan òg uttrykkast ved hjelp av polarkoordinatar gjennom formelen:
Der e er eksentrisiteten. og er semi latus rectum
Dersom e > 1, vil likninga gje ein hyperbel; e = 1 gjev ein parabel medan e < 1 gjev ein ellipse. Spesialtilfellet e = 0 vil gje ein sirkel mad radius .
Bruk i tre dimensjonar[endre | endre wikiteksten]
Polarkoordinatar kan òg nyttast til bruk i tre dimensjonar. Kulekoordinatar og sylinderkoordinatar inneheld begge polarkoordinatplanet, utvida med ein ekstra akse.
Sylinderkoordinatar[endre | endre wikiteksten]

Sylinderkoordinatsystemet er ei utviding av polarkoordinatar med ein ekstra z-akse, på same måte som det kartesiske koordinatsystemet i tre dimensjonar. Den tredje koordinaten er vanlegvis uttrykt med ein h eller ein z, som skildrar høgda til det øvre planet i sylinderen. Alle tre koordinatane blir då skrive (r, θ, h).
Samanhengen mellom dei tre sylinderkoordinatane og dei respektive kartesiske koordinatane blir
Kulekoordinatar[endre | endre wikiteksten]

Kulekoordinatsystemet er eit koordinatsystem basert på polarkoordinatar. Kulekoordinatar skil seg frå polarkoordinatar ved at høgda frå xy-planet blir skildra av ein vinkel φ frå z-aksen, og at radiusen på xy-planet r er skildra med ρ som er radiusen frå origo til flata til ein lekam på eit vilkårleg punkt. Vinkelen til φ varierer med storleikane 0°-180° eller 0-π radianar. Alle dei tre koordinatane blir då skrive (ρ, θ, φ).
Samanhengen mellom dei tre kulekoordinatane og dei respektive kartesiske koordinatane blir;
Kjelder[endre | endre wikiteksten]
- Denne artikkelen bygger på «Polarkoordinatsystem» frå Wikipedia på bokmål, den 9. januar 2012.






![{\displaystyle \left.{\begin{matrix}x=r\cdot \cos(\varphi )\\y=r\cdot \sin(\varphi )\end{matrix}}\right\}\quad ,r=1\quad ,\quad \varphi \in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e684d6b1b16ad2845e4cc0ca2f1202d231607eb)







