Oktaeder

(animasjon)

Ein oktaeder bretta ut i ei todimensjonal flate.

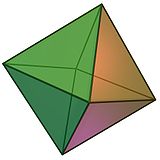
Oktaeder er eit polyeder med åtte sideflater, men vanlegvis vert det meint eit regulært oktaeder: ein platonsk lekam sett saman av åtte trekanta sideflater. Desse overflatene er likesida trekantar. I tillegg har den seks hjørne og tolv kantar.

Areal og volum

Viss $a$ i eit regulært oktaeder er kant, kan arealet og volumet reknast ut slik:

$A=2\sqrt{3}a^2 \approx 3.46410162a^2$

$V=\frac{1}{3} \sqrt{2}a^3 \approx 0.471404521a^3$

Radius

Viss $a$ i eit regulært oktaeder er kant, er radiusen av ei kule som akkurat fyller ut hele figuren:

$r_u = \frac{a}{2} \sqrt{2} \approx 0.7071067 \cdot a$

Radiusen av den største kula som kan innskrivast i det er:

$r_i = \frac{a}{6} \sqrt{6} \approx 0.4082482\cdot a$

Midtradiusen, dvs. radiusen av ei kule der flata rører midten av kvar kant, er:

$r_m = \frac{a}{2} = 0.5\cdot a$

Avkuttingssekvens

Tetraeder

Avkutta tetraeder

Oktaeder

Avkutta tetraeder

Tetraeder

Sjå òg

• Platonsk lekam
• Trekant