Det gylne snittet

Det gylne snittet vil seie deling av ei linje eller ei flate i to delar slik at den minste delen står i høve til den største som denne til heile linja eller flata.
Uttrykt som φ (phi) tilsvarar dette eit irrasjonalt tal med verdi
Ein kan finne dette delingsforholdet igjen mange stader i naturen, og spesielt på menneskekroppen. Tilhøvet mellom lengda frå skuldra til fingertuppane og lengda frå olbogen til fingertuppane, knokane på handa og lengda på beina i tilhøve til lengda frå kneet til tærne er nokre døme. Det er òg eit viktig visuelt verkemiddel innan kunst. Det gylne snittet var kjent blant dei gamle grekarane. Det vart mykje brukt i renessansen, særleg innan arkitektur.
Å dele ei linje etter det gylne snittet vert òg kalla høgdeling.
Matematikk[endre | endre wikiteksten]

2. Teikn ei linje frå midtpunktet på ei av sidene til eit motståande hjørne.
3. Teikn ein boge med denne linja som radius så dei til saman utgjer den lange sida i rektangelet.
Det gylne snittet byggjer på ei harmonisk deling av eit linjestykke. Snitta deler linjestykket slik at tilhøvet mellom den lengste og den kortaste delen er like stort som tilhøvet mellom heile linjestykket og den lengste delen av det.
Matematisk kan dette uttrykkjast slik: Viss linjestykket AB er delt i eit punkt S slik at tilhøvet mellom AB og AS er lik tilhøvet mellom AS og BS seier ein at S deler AB i det gylne snittet

Av definisjonen:
Den høgre likninga viser at , som kan bli sett inn i den venstre halvdelen, som då gjev:
Stryke ut b og multiplisere begge sider med φ og ordne likninga fører til:
Det kan enkelt verifiserast at den einaste positive løysinga til denne andregradslikninga er
Det motsette forholdet er kjent som det konjugerte gylne snittet og ein brukar stor Φ for å gje dette som ():
Alternativt kan uttrykkast som:
Dette illustrer den unike eigenskapen (blant positive tal) med det gylne snittet at:
Dei to løysingane er innbyrdes inverse og har de same desimalane.
Kunst[endre | endre wikiteksten]

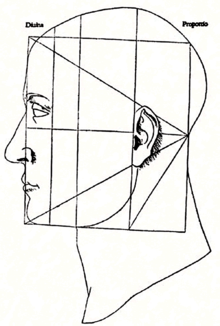
Leonardo da Vinci (1452–1519) opna ei av bøkene sine med følgjande utsegn: «La ingen som ikkje er matematikar lese arbeidet mitt!». Denne spissformuleringa viser interessa til kunstnaren for matematikkfaget. Ved sida av å interessere seg for geometri, studerte han menneskekroppen særs inngåande. Han fann mange tilhøve på menneskekroppen som, ifølgje han sjølv, burde vere lik det gylne snittet for at det skulle vere ein perfekt kropp. Da Vinci hevda at tilhøvet mellom høgda frå navlen og ned og høgda frå navlen og opp bør vere lik det gylne snittet. Det tyder at ein person på 150 cm, skal ha ei navlehøgd på kring 93 cm
Mange biletkunstnarar har, medvite eller umedvite, forhalde seg til det gylne snittet i verka sine. Piet Mondrian arbeidde ofte lenge med elementa i sine Tableaux. Om han målte seg fram eller ikkje, veit ingen, men dei fleste delelinjene i desse bileta fell saman med gylne snittproporsjonar.
Eit BBC-program om andlet og venleik handla i stor utstrekking om at andlet som hadde flatene fordelt etter det gylne snittet vart rekna av det breie publikummet som meir tiltalande enn andlet som ikkje var det. Dei fleste populære skodespelarar og modellar i dag fell inn under denne «norma».
Tidslinje[endre | endre wikiteksten]
- Phidias (490–430 f.Kr) laga Parthenon-statuen som har gylne snitt-proporsjonar.
- Platon (427–347 f.Kr) skildra i Timaios fem moglege former no kjent som platonske lekamar (pyramide, kube, oktaeder, dodekaeder og ikosaeder), der nokre er relatert til det gylne snittet.
- Euklid (ca. 365–265 f.Kr), i sin første Elementa, gav den første oppteikna definisjonen av det gylne snittet som han kalla «ακρος και μεσος λογος». Seinare vart dette omsett til «proportio habens medium et duo extrema», som i dag vert omsett som «deling i indre og ytre tilhøve».[2]
- Luca Pacioli (1445–1517) definerte det gylne snittet som eit «guddommeleg tilhøve» i sin Divina Proportione.
- Johannes Kepler (1571–1630) skildrar det gylne snittet som ein «verdifull juvel»: «Geometri har to store skattar: ein er Pythagoras' teorem, og det andre er delinga av ei linje i ytre og indre tilhøve. Det første kan samanliknast med ei skjeppe gull; det andre kan vi kalle ein verdifull juvel.»
- Charles Bonnet (1720–1793) poengterte at i spiralen av bladstillinga til planter som blir forma med og mot klokka ofte har fibonaccitala som forholdstal.
- Martin Ohm (1792–1872) trur ein er den første som nytta uttrykket «det gylne snittet» for å skildre dette tilhøvet.
- Edouard Lucas (1842–1891) gav den numeriske sekvensen kjent som Fibonaccifølgja dagens namn.
- Marker Barr (1900-talet) tilordna den første bokstaven i det greske namnet Phidias til det gylne snittet.
- Roger Penrose (fødd 1931) fann ein symmetri som nyttar det gylne snittet i feltet aperiodisk tesselering, noko som førte til oppdaginga av kvasikrystallar.
Kjelder[endre | endre wikiteksten]
- Denne artikkelen bygger på «Det gylne snitt» frå Wikipedia på bokmål, den 13. september 2011.
- Wikipedia på bokmål oppgav desse kjeldene:
- Wikipedia på bokmål oppgav desse kjeldene:
- ↑ Hemenway, Priya (2005). Divine Proportion: Phi In Art, Nature, and Science. New York: Sterling. s. 20–21. ISBN 1-4027-3522-7.
- ↑ Heath, Thomas L. (1956): The Thirteen Books of Euclid's Elements, Book 6, Definition 30, Dover Publication, New York. ISBN 0-486-60089-0 ss. 267-268
Litteratur[endre | endre wikiteksten]
- Arakelian, Hrant: Mathematics and History of the Golden Section. Logos 2014, 404 p. ISBN 978-5-98704-663-0 (rus.).
- Blatner, David: The joy of Pi.
- Dalvang, Tone og Rohde, Vetle: Matematikk for alle. Landslaget for matematikk i skolen, Landås 1998.
- Eibe, Thyra: Euklids Elementer. Omsett av Thyra Eibe. København, Gyldendal ; 1897-1917.
- Høyrup, Jens: Sub-Scientific Mathematics. History of Science, vol 28, 1979.
- Jama, Jama Musse: Ethnomathematics.
- Knott, Ron: Fibonacci Numbers and the Golden Section.
- Krause, M.: Multicultural mathematics material, NCTM 1983.
- Levin, Eddy: The Golden Proportion.
- Rossing, Nils Kr.: Den matematiske krydderhylle. Tapir akademisk forlag (7. utgåve), 2007.
- Selvik, Bjørg K. (red): Matematiske sammenhenger: Geometri. Caspar forlag, 1999.
- Stewart, Ian: Life's other secret - The new Mathematics of Living World. Penguin books, 1999.










