Flatevidd

Flatevidd eller areal er ord som vert brukte for å uttrykka utstrekkinga av eit område.
Einingane ein bruker til å måle flatevidd har to dimensjonar, lengde og breidde. Ein kvadratmeter er til dømes ein meter lang og ein meter brei, medan ein kvadratkilometer er ein kilometer i kvar retning. Andre einingar ein ofte brukar for å snakka om flatevidd er mål og dekar, som begge er definert som 1000 kvadratmeter.
Det er fleire kjende formlar for enkle former som trekantar, rektangel og sirklar. Ved å nytte desse formlane kan ein finne arealet til alle polygon ved å dele dei inn i trekantar.[1] For former som består av kurver, må ein som regel nytte differensialrekning for å finne arealet. Faktisk var problemet med å finne arealet til forskjellige figurar ein stor motivasjonsfaktor for utviklinga av differensialrekning.[2]
For former som kuler, kjegler og sylindrar, vert arealet av overflata kalla overflatearealet. Formlar for overflateareal av enkle former vart rekna ut av greske matematikarar i antikken.
Formell definisjon[endre | endre wikiteksten]
Ei tilnærming til å definere kva ein meiner med areal finn ein gjennom aksioma. Til dømes kan ein definere eit areal som ein funksjon a frå ei samlnig M av ei særskild plan figur i ei mengd reelle tal som tilfredsstiller følgjande eigenskapar:
- For alle S i M, .
- Om S og T er i M så er òg og det, .
- Om S og T er i M med så er T − S i M og a(T − S) = a(T) − a(S).
- Om ei mengd S er i M og S er kongruent til T så er T òg i M og a(S) = a(T).
- Alle rektangel R er i M. Om rektangelet har lengda h og breidda k så er a(R) = hk.
- La Q vere ei mengd lukka mellom to stegvise regionar S go T. Ein stegregion er danna av ein endeleg union av tilstøytande rekangel som kviler på same grunnlinje, til dømes . Om det finst eit unikt tal c slik at for alle slike stegregionar S og T, så er a(Q) = c.
Einingar[endre | endre wikiteksten]

Kvar lengdeeining har ein tilsvarande eining for areal, nemleg arealet til eit kvadrat med den lengda ein har nytta. Areal kan derfor målast i kvadratmeter (m2), kvadratcentimeter (cm2), kvadratmillimeter (mm2), kvadratkilometer (km2), kvadratfot (ft2), kvadratyard (yd2), kvadratmile (mi2), og så vidare. Algebraisk kan ein tenkje på desse einingane som kvadrat av dei samsvarande lengdeeiningane.
SI-eininga for areal er kvadratmeter.
Omrekningar[endre | endre wikiteksten]
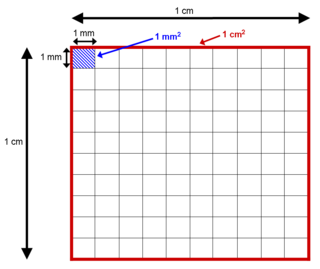
Omrekninga mellom to arealeiningar er kvadratet av omrekninga mellom dei tilsvarande lengdeeiningane. Til dømes sidan
så er forholdet mellom kvadratfot og kvadrattomme
- 1 kvadratfot = 144 kvadrattommar
der 144 = 122 = 12 × 12. På liknande vis:
- 1 kvadratkilometer = 1 000 000 kvadratmeter
- 1 kvadratmeter = 10 000 kvadratcentimeter = 1 000 000 kvadratmillimeter
- 1 kvadratcentimeter = 100 kvadratmillimeter
- 1 kvadratyard = 9 kvadratfot
- 1 kvadratmile = 3 097 600 kvadratyard = 27 878 400 kvadratfot
I tillegg,
- 1 kvadrattomme = 6,4516 kvadratcentimeter
- 1 kvadratfot = 0.09290304 kvadratmeter
- 1 kvadratyard = 0.83612736 kvadratmeter
- 1 kvadratmile = 2.589988110336 kvadratkilometer
Andre einingar[endre | endre wikiteksten]
Det finst òg fleire andre einingar for areal.
Hektar eller mål vert ofte framleis nytta for å måle landområde
- 1 hektar = 10 000 kvadratmeter = 0.01 kvadratkilometer
I somme land nyttar ein òg acre der
- 1 acre = 4 840 kvadratyard = 43 560 kvadratfot
Ein acre er om lag 40 % av ein hektar.
Arealformlar[endre | endre wikiteksten]
Rektangel[endre | endre wikiteksten]

Den mest grunnleggande arealformelen er formelen for arealet til eit rektangel. Eit rektangel med lengda l og breidda b, har arealformelen:
- A = lb (rektangel).
Altså arealet er lengda multiplisert med breidda. Eit spesialtilfelle er eit kvadrat med lengda s som er gjeven av formelen
- A = s2 (kvadrat).

Oppdelingsformlar[endre | endre wikiteksten]
Dei fleste andre enkle formlar for areal går ut på å dele opp problemet. Dette vil sei å dele formene inn i bitar som ein kan rekne ut arealet for, og så summere arealet for å få arealet til den originale forma.
Til dømes kan eit parallellogram delast inn i eit trapes og ein rettvinkla trekant, som vist i figuren til venstre. Om trekanten vert flytta til den andre sida av trapeset får ein eit rektangel. Dermed vil arealet til parallellogrammet vere det same som arealet til rektangelet:
- A = bh (parallellogram).
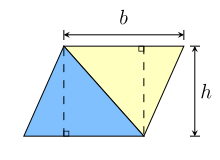
Det same parallellogrammet kan kuttast inn i ein diagonal og delast inn i to kongruente triangel, som synt i figuren til høgre. Det følgjer at arealet kvart triangel er halvparten av arealet til parallellogrammet:
- (trekant).
Liknande argument kan nyttast til å finne arealformlar for trapes og rombe, samt meir kompliserte polygon.
Sirklar[endre | endre wikiteksten]

Formelen for arealet til ein sirkel er basert på ein liknande metode. Om ein har ein sirkel med radius r, er det mogeleg å dele sirkelen inn i sektorar, som vist i figuren til høgre. Kvar sektor er tilnærma trekantforma og kan omarrangerast og forme eit tilnræma parallellogram. Høgda på dette parallellogrammet er r, og breidda er halve omkrinssen til sirkelen eller πr. Dermed er det totale arealet til sirkelen r × πr, eller πr2:
- A = πr2 (sirkel).
Sjølv om oppdelinga nytta i denne formelen berre er ei tilnærming, vert feilen mindre og mindre etter fleire og fleire sektorar ein deler sirkelen inn i. Grensa til arealet for det tilnærma parallellogrammet er nøyaktig πr2, som er arealet for ein sirkel.
Denne metoden er faktisk eit enkelt døme på ideane i differensialrekning.
Overflateareal[endre | endre wikiteksten]

Dei mest grunnleggande formlane for overflateareal kan ein få ved å kutte overflata opp og flate dei ut. Til dømes om overflata til ein sylinder (eller eit prisme) vert kutta på langs, så kan ein brette ut overflata til eit rektangel. På liknande vis kan ein kutte langs sida på ei kjegle og få ein sektor av ein sirkel, som så kan reknast ut.
Formelen for overflatearealet til ei kule er vanskelegare, fordi overflate har ei ei gaussisk krumming som ikkje er lik null, og dermed ikkje kan flatast ut. Formelen for overflate arealet til ei kule var det Arkimedes som først kom fram til i verket On the Sphere and Cylinder. Formelen er
- A = 4πr2 (kule).
der r er radiusen til kula. Som med formelen for arealet til ein sirkel kan ein kome fram til denne formelen med liknande metodar som vert nytta i differensialrekning.
Formlar[endre | endre wikiteksten]
| Form | Formel | Variablar |
|---|---|---|
| Likesida trekant | er lengda til ei side i trekanten. | |
| Trekant | er halve omkrinsen, , og er lengda på kvar side. | |
| Trekant | og er to vilkårlege sider og er vinkelen mellom dei. | |
| Trekant | og er høvesvis grunnlinja og høgda (målt vinkelrett på grunnlinja). | |
| Kvadrat | er lengda til ei side av kvadratet. | |
| Rektangel | og er lengdene til sidene i rektangelet (lengda og breidda). | |
| Rombe | og er lengda til dei to diagonalane i romben. | |
| Parallellogram | er lengda til grunnlinja og er høgda som står vinkelrett på grunnlinja. | |
| Trapes | og er lengda til dei parallelle sidene og er avstanden (høgda) mellom parallellane. | |
| Likesida sekskant | er lengda til ei av sidene i sekskanten. | |
| Likesida åttekant | er lengda til ei av sidene i åttekanten. | |
| Likesida polygon | er lengda til ei side og er mengda sider. | |
| Likesida polygon | er omkrinsen og er mengda sider | |
| Likesida polygon | er radiusen til ein omskriven sirkel, er radiusen til ein innskriven sirkel og mengda sider. | |
| Likesida polygon | er radiusen til ein innskriven sirkel og er omkrinsen til polygonet. | |
| Sirkel | er radiusen og er diameteren. | |
| Sirkelsektor | og er høvesvis radiusen og vinkelen (i radianar). | |
| Ellipse | og er høvesvis lengda på den vesle og den store aksen. | |
| Totalt overflatearealet av ein sylinder | og er høvesvis radius og høgd. | |
| Overflatearealet til ei sylinderside. | og er høvesvis radius og høgd. | |
| Det totale overflatearealet til ei kjegle | og er høvesvis radius og skråhøgda. | |
| Overflate til ei kjegleside | og er høvesvis radius og skråhøgda. | |
| Overflatearealet til ei kule | og er høvesvis radius og diameter. | |
| Det totale overflatearealet til ein ellipsoide | Sjå artikkelen. | |
| Det totale overflatearealet til ein pyramide | er grunnarealet, er omkrinsen til grunnflata og er skråhøgda. | |
| Omforming frå kvadratisk til sirkulært areal. | er arealet til kvadratet i kvadrateiningar. | |
| Omforming frå sirkel til kvadratareal | er arealet til sirkelen i sirkeleiningar. |
Andre formlar[endre | endre wikiteksten]
Areal i differensialrekning[endre | endre wikiteksten]
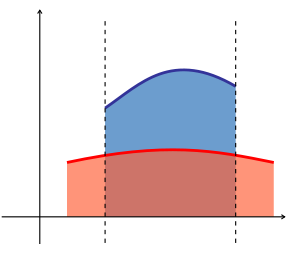
- arealet mellom grafane til to funksjonar er lik integralet til den eine funksjonen, f(x), minus integralet til den andre funksjonen, g(x).
- eit areal avgrensa av ein funksjon r = r(θ) uttrykt i polarkoordinatar er .
- arealet lukka av ei parametrisk kurve med endepunkt er gjeven av linjeintegrala
- eller z-komponenten av
Generell formel for overflateareal[endre | endre wikiteksten]
Den generelle formelen for overflatearealet av grafen til ein kontinuerleg differensierbar funksjon der og er ein region i xy-planet med glatte grenser:
Ein enno meir generell formel for arealet til ein graf av ei parametrisk flate på vektorforma der er ein kontinuerleg differensierbar vektorfunksjon av :
Kjelder[endre | endre wikiteksten]
- Denne artikkelen bygger på «Area» frå Wikipedia på engelsk, den 29. oktober 2011.
- Wikipedia på engelsk oppgav desse kjeldene:
- ↑ Mark de Berg; Marc van Kreveld; Mark Overmars; Otfried Schwarzkopf (2000), «3: Polygon Triangulation», Computational Geometry (2. revidert utg.), Springer-Verlag, s. 45–61, ISBN 3-540-65620-0
- ↑ Boyer, Carl B. (1959). A History of the Calculus and Its Conceptual Development. Dover. ISBN 0-486-60509-4.
- ↑ do Carmo, Manfredo. Differential Geometry of Curves and Surfaces. Prentice-Hall, 1976. Side 98.
Bakgrunnsstoff[endre | endre wikiteksten]
| Slå opp flatevidd i Wiktionary, den frie ordboka. |
- Weisstein, Eric W., «Area» frå MathWorld.
- Arealformlar
































































