Potensiell energi

Potensiell energi (stillingsenergi) er den lagra energien til ein lekam i eit fysisk system.[1] Denne typen energi har potensialet til å endre tilstanden til andre lekamar rundt seg, til dømes utforminga eller rørsla.
Ein har forskjellige former for energi som kan kallast potensiell energi. Alle desse formene er assosiert med ei spesiell kraft som påverkar ein fysisk eigenskap av stoffet (slik som masse, lading, elastisitet, temperatur osv.). Til dømes er den potensielle energien som skuldast gravitasjon assosiert med tyngdekrafta som verkar på lekamen sin masse. Elastisk potensiell energi kjem av elastiske krefter (til sjuande og sist elektromagnetiske krefter). Elektrisk potensiell energi er assosiert med Coulomb-krafta. Nukleære krefter verkar på den elektriske ladinga. Kjemisk potensiell energi er assosiert med det kjemiske potensialet til ei spesifikk atom- og molekylsamansetjing, som verkar på strukturen til det kjemiske stoffet som lekamen er bygd opp av. Termisk potensiell energi er assosiert med elektromagnetiske krefter i samsvar med temperaturen til lekamen.
Potensiell energi som skuldast tyngdekraft[endre | endre wikiteksten]
Potensiell energi som skuldast tyngdekraft er potensiell energi som ein lekam har i kraft av massen sin og tyngdekrafta som verkar på han.
I det daglege oppstår denne typen potensiell energi når ein lekam vert heva i jorda sitt tyngdefelt. Auken i den potensielle energien til lekamen er lik energien som må til for å heve han, eller lik energien som vert frigjeven om han fekk falle tilbake til det opphavlege nivået.

Til dømes kan ein tenkje seg ei bok som er plassert på eit bord. For å heve boka frå golvet til bordet må ein gjere eit arbeid, som krev energi (om boka vart løfta av ein person så vil denne energien kome frå den kjemiske energien som personen får frå mat). Viss ein tenkjer seg at effektiviteten er perfekt (ikkje energitap), er energien som vert brukt på å løfte boka nøyaktig den same som auken i boka sin potensielle energi. Boka sin potensielle energi kan verte frigjeven om ho fell ned frå bordet. Når boka fell vert den potensielle energien omgjort til kinetisk energi, og når boka treffer golvet vert den kinetiske energien igjen omgjort til varme og lyd.
Faktorane som påverkar den potensielle energien som skuldast tyngdekrafta er høgda som lekamen vert heva til, massen og styrken til tyngdefeltet. Derfor har ei bok som ligg på eit bord mindre potensiell energi som følgje av tyngdekrafta enn ei bok som ligg på eit høgare bord, eller i tyngre bok som ligg på same bordet. Når ein lekam har mindre potensiell energi som følgje av tyngdekrafta på Månen i forhold til energien han ville hatt på jorda, så kjem det av at tyngdefeltet på månen er svakare. (Tyngdekrafta mellom to lekamar er direkte proporsjonal med produktet av massane deira og omvendt proporsjonal med avstanden mellom dei i følgje Newton si gravitasjonslov.
Utrekning av potensiell energi som skuldast tyngdekrafta[endre | endre wikiteksten]
Ein tenkjer seg at tyngdekreftene mellom lekamane er konstant, og at arbeidet som vert gjort for å heve ein lekam er lik krafta multiplisert med avstanden som lekamen vert heva. Tyngdekrafta som må overvinnast er lik massen til lekamen multiplisert med tyngdeakselerasjonen, slik at lekamen sin potensielle energi som følgje av tyngdekrafta Ug er gjeven ved
der
- m er massen til lekamen
- g er tyngdeakselerasjon (om lag 9,81 m/s2 på jordoverflata)
- h er høgda lekamen har vorte heva relativt til eit referansenivå (som jordoverflata).
Resultatet vert uttrykt i joule (kg m2/s2).
Likninga viser at den potensielle energien er proporsjonal til både massen og høgda. Til dømes må ein ha same energimengda for å heve to like tunge lekamar, som å heve ein lekam dobbelt så høgt.
«mgh»-formelen fungerer så lenge tyngdeakselerasjonen, g, er tilnærma konstant over avstanden h. Nær jordoverflata er denne tilnærminga god, men er det snakk om store avstandar, til dømes romfartøy og astronomiske lekamar, så held den ikkje mål.
For å rekne ut den potensielle energien som følgje av tyngdekrafta når g varierer, kan ein dele opp avstanden i «uendeleg» mange delar, og leggje saman den potensielle energien med varierande g for kvar del. Denne summen vert då eit integral.
For å gjere evalueringa av integralet lettare, kan ein tenkje seg at tyngdekreftene verkar som om massen til lekamen er konsentrert i massesenteret til lekamen. Denne føresettinga er matematisk korrekt for kulerunde lekamar (tilnærma ein planet til dømes). Ho gjeld vanlegvis ikkje i andre tilfelle, bortsett frå om avstanden mellom lekamane er så store at lekamane kan reknast som to punkt.
Med denne enklare føresettinga fører integreringa over avstanden mellom lekamane til ein potensiell energi for dei to massane lik:
der
- og er massane til dei to lekamane
- er gravitasjonskonstanten (som ikkje er den same som g nemnd tidlegare)
- er referanse nivået
- er den faktiske avstanden mellom lekamane.
og er altså målt mellom massesenteret til dei to lekamane.
I eit tilfelle der ein har ein liten lekam over jordoverflata, der overflata er referansenivået, er og massen til Jorda og til lekamen, er avstanden frå senteret av jorda til jordoverflata, og er avstanden frå jordoverflata til lekamen.
Viss ein prøver å rekne ut ein «absolutt» potensiell energi ved å setje referansenivået lik null, så «eksploderer» formelen fordi vi deler på null. Med andre ord kan ein berre bruke denne formelen for å måle skilnaden i potensiell energi mellom to lekamar.
I praksis er det ofte nyttig å setje referansenivået til uendeleg (t.d. ), og då vert likninga:
der r no er avstanden mellom massesenteret til dei to lekamane. For ein liten lekam over jordoverflata, vert r no avstanden frå lekamen til jordsenteret.
Ved å bruke denne metoden vert den potensielle energien lik null når r er stor nok, og negativ for endelege verdiar av r. Skilnaden i den potensielle energien – som er storleiken vi eigentleg er interessert i – er derimot positiv.
Ug måler den potensielle energien til heile systemet, når den vert utrekna som over. Viss ein tenkjer seg at to lekamar i rommet vert halde på plass og så slept laus slik at tyngdekreftene mellom dei dreg dei mot kvarandre, så vil summen av den kinetiske energien til dei to lekamane vere nøyaktig lik minkinga av den potensielle energien i systemet. Summen av den kinetiske energien som dei to lekamane får er lik den resiproke verdien av forholdet mellom massane deira. Så i tilfelle der ein lett lekam fell mot ein stor og massiv lekam (slik som jorda), så vert så godt som all den potensielle energien i systemet overført til den lette lekamen, og nesten ingenting til den store lekamen.
Sjå òg tolekamproblem og gravitasjonsbindingsenergi.
Tyngdepotensial[endre | endre wikiteksten]
Tyngdepotensial er den potensielle energien per masseeining til ein lekam som følgje av plasseringa i eit tyngdefelt. Tyngdepotensialet på grunn av ei punktmasse er:
der:
- er universell gravitasjonskonstant,
- er avstanden til massesenteret til lekamen.
- er massen til lekamen.
I romfartsdynamikk må tyngdepotensialfunksjonen ha med dei ikkje-sfæriske og ikkje-homogene eigenskapane til vanlege kjelder til tyngdepotensialet. I dette tilfellet kan tyngdepotensialet vere avhengig av polar - og asimut -retning av vektor .
Den mest brukte forma av tyngdepotensialfunksjonen er avhengig av (breiddegrad) og potensialkoeffisienten, Jn, kalla sonal koeffisient:
Elastisk potensiell energi[endre | endre wikiteksten]
- For meir om dette emnet, sjå Elastisk potensiell energi.
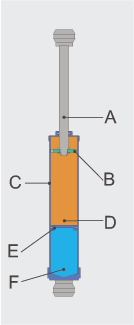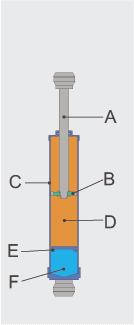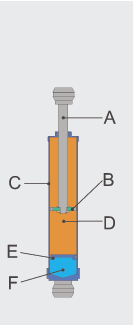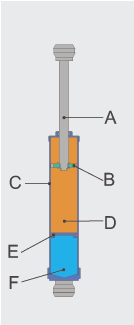
Elastisk potensiell energi er den potensielle energien til ein elastisk lekam (t.d. ein boge eller ein katapult), som vert deformert under stramming eller kompresjon (ofte kalla fysisk stress). Energien oppstår som følgje av ei kraft som prøver å gjenopprette den opphavlege forma til lekamen. Denne krafta er som oftast den elektromagnestiske krafta mellom atom og molekyl i lekamen.
Utrekning av elastisk potensiell energi[endre | endre wikiteksten]
Me tenkjer oss ei fjør med naturleg lengde l og elastisitetsmodul λ, som vert strekt ut lengda x. Den elastiske potensielle energien kan då reknast ut med denne likninga:
Denne likninga får ein ved å integrere Hooke si lov:
Likninga vert ofte brukt for å rekne ut posisjonen til mekanisk likevekt.
Generelt vert den elastiske energien gjeven ved Helmholtz-potensialet per volum f som ein funksjon av strekktensorkomponentane εij:
Der λ og μ er Lamé elastiske koeffisientar. Samanhengen mellom stresstensorkomponentane og strekktensorkomponentane er:
For eit stoff med youngsmodul Y (same som elastisitetsmodul λ), tverrsnittareal A0, normal lengd l0, som vert strekt lengda har ein:
- der Ue er elastisk potensiell energi.
Den elastiske potensielle energien per volum er gjeven ved:
- der er strekket i stoffet.
Kjemisk energi[endre | endre wikiteksten]
Kjemisk energi er ein type potensiell energi relatert til den strukturelle samansettinga av atom eller molekyl. Denne samansettinga kan kome av kjemiske bindingar i eit molekyl og elles. Kjemisk energi i eit kjemisk stoff kan omformast til andre former for energi gjennom ein kjemisk reaksjon. T.d. når noko brenn vert den kjemiske energien omgjort til varme, og det same er tilfellet med fordøying av mat i biologiske organismar. Grøne planter omformar solenergi til kjemisk energi gjennom ein prosess kalla fotosyntese, og elektrisk energi kan omformast til kjemiske energi gjennom elektrokjemiske reaksjonar.
Det liknande uttrykket kjemisk potensial vert brukt av kjemikarar for å indikere potensialet eit stoff har for å gjennomgå ein kjemisk reaksjon.
Elektrisk potensiell energi[endre | endre wikiteksten]
- For meir om dette emnet, sjå Elektrisk energi.
Ein lekam kan òg ha potensiell energi i kraft av den elektriske ladinga til lekamen og fleire krefter som oppstår som følgje av ladinga. Det finst tre forskjellige typar av denne forma for potensiell energi: Elektrostatisk potensiell energi, elektrodynamisk potensiell energi (av og til kalla magnetisk potensiell energi) og nukleær potensiell energi.

Elektrostatisk potensiell energi[endre | endre wikiteksten]
Når den elektriske ladinga til ein lekam er i ro, har lekamen ein potensiell energi i forhold til andre ladde lekamar.
Elektrostatisk potensiell energi er energien til ein elektrisk ladd partikkel i eit elektrisk felt. Han er definert som fysisk arbeid som kravst for å flytte partikkelen frå ein uendeleg avstand og til den noverande posisjonen, utan at andre elektriske krefter verkar på lekamen. Denne energien er ulik null om det er ein anna elektrisk ladd lekam i nærleiken.
Det enklaste dømet er når ein har to punktliknande lekamar A1 og A2 med elektrisk ladingar q1 og q2. Arbeidet W som må til for å flytte A1 frå eit punkt uendeleg langt borte til eit punkt med avstand d til A2 er gjeve med:
der k er Coulomb-konstanten, som er lik .
Likninga får ein ved å integrere Coulombkrafta mellom grensene uendeleg og d.
Eit relatert mål kalla elektrisk potensial er lik elektrisk potensiell energi dividert på elektrisk lading.
Elektrodynamisk potensiell energi[endre | endre wikiteksten]
Når ein ladd lekam eller dei tilhøyrande ladde partiklane ikkje er i ro, vert det generert eit magnetfelt som medfører ei anna form for potensiell energi, ofte kalla magnetisk potensiell energi. Denne forma for potensiell energi kjem av fenomenet kalla magnetisme, der ein lekam er magnetisk og har potensialet til å flytte liknande lekamar. Magnetiske felt og studiet av desse kjem inn under elektrodynamikk.
Nukleær potensiell energi[endre | endre wikiteksten]
Nukleær potensiell energi er den potensielle energien til kjernepartiklar i ei atomkjerne, der enkelte av dei har elektrisk lading. Denne forma for potensiell energi er forskjellig frå dei to andre elektriske potensielle energiane, fordi i dette tilfellet er dei ladde partiklane ekstremt nær kvarandre. Kjernepartiklane er knytt saman av sterke nukleære krefter. Svake nukleære krefter gjev den potensielle energien for visse typar av radioaktiv nedbryting, slik som betanedbryting.
Kjernepartiklar som proton og nøytron vert ikkje øydelagd i fisjon- og fusjonsprosessar, men samlingar av dei har mindre masse enn dei individuelle partiklane, og denne masseskilnaden vert frigjeven som varme og stråling i kjernereaksjonar. Energien frå Sola, kalla solenergi, er eit døme på denne forma for energiomforming. I Sola fusjonerer hydrogen og rundt 4 millionar tonn solmasse vert omforma til lys kvart sekund, som vert strålt ut i verdsrommet.
Termisk potensiell energi[endre | endre wikiteksten]
Ein lekam kan òg endre rørsla til andre lekamar i kraft av temperaturen og den elektromagnetiske krafta til lekamen, gjennom stråling. Denne forma for potensiell energi vert kalla termisk potensiell energi.
Kvilemasseenergi[endre | endre wikiteksten]
Albert Einstein sin vidkjende formel, som vart utleia i den spesielle relativitetsteorien, kan skrivast:
der E0 er kvilemasseenergien, m er kvilemassen til lekamen, og c er lysfarten i vakuum.
Kvilemasseenergien er energimengda som ligg i massen når han ligg i ro. Likninga viser samanhengen mellom masse og energi, og sjølv ein liten masse inneheld enorme energimengder (t.d. 90 petajoule per kilo ≈ 21 megatonn TNT per kilo)
Forholdet mellom potensiell energi og kraft[endre | endre wikiteksten]
Potensiell energi er nært knytt til fysisk kraft. Viss arbeidet som er gjort når ein lekam har flytta seg langs ein bane som byrjar og sluttar på same stad, så er krafta konservativ, og ein kan definere ein numerisk verdi for potensialet knytt til kvart punkt i rommet. Eit kraftfelt kan ein få ved å ta vektorgradienten av potensialfeltet.
Til dømes er gravitasjon ei konservativ kraft. Arbeidet som vert gjort per masse frå eit punkt A med til punkt B med av gravitasjonen, er og arbeidet som vert gjort ved å gå tilbake same vegen er , slik at det totale arbeidet frå
Viss vi omdefinerar potensialet i A til å vere og potensialet i B til å vere (der er kva som helst nummer, både positivt og negativt, men det må vere same tal i alle punkt) så er arbeidet gjort ved å gå frå
som før.
I praksis betyr dette at ein kan sette lik null kor hen ein vil, til dømes ved jordoverflata.
Ein ting å leggje merke til når det gjeld konservative krefter er at arbeidet som vert gjort ved å gå frå A til B ikkje er avhengig av kva veg ein tar. Visst det hadde noko å sei ville det vore meiningslaust å definere eit potensial for kvart punkt i rommet, og det gjev ikkje meining å definere eit potensial assosiert med friksjon.
Alle døma som er nemnd over er eigentleg energi lagra i eit kraftfeltet. I elastisk potensiell energi så vert atoma tvunge litt frå kvarandre når ein strekker eit elastisk stoff. Kraftige elektromagnetiske krefter prøver å halde atoma i deira optimale avstand frå kvarandre, slik at elastisk potensial eigentleg er eit elektromagnetisk potensial. Forskarar snakkar derimot sjeldan om krefter på atomskala, og det meste vert uttrykt i form av energi i staden for krefter.
Kjelder[endre | endre wikiteksten]
- ↑ Rosvold, Knut A.; Grøn, Øyvind; Hofstad, Knut (14. november 2020). «potensiell energi». Store norske leksikon (på norsk bokmål).
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6. utg.). Brooks/Cole. ISBN 0-534-40842-7.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5. utg.). W. H. Freeman. ISBN 0-7167-0809-4.



















![{\displaystyle E(r,\phi )={\frac {GM}{r}}\left[1-\sum _{n=2}^{N}J_{n}\left({\frac {R}{r}}\right)^{2}P_{n}(\sin \phi )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aa5f192466a9402b28b37fc0b7962401489cf2f)




















