Arkimedisk lekam
Ein arkimedisk lekam er innan geometri ein tredimensjonal lekam (polyeder) som består av to eller fleire polygonar som møtest i like hjørne.[1] Dette skil seg frå platonske lekamar som består av like polygonar som møtest i like hjørne, og katalanske lekamar kor det er sidene som er like og kantane ulike.
Pseudorombkuboktaederet er eit særtilfelle. Den har rettnok «like hjørne», men dei står ikkje i ein symmetrisk stilling, som ein kunne forvente av både platonske, arkimediske og katalanske lekamar. Dermed kan pseudorombkuboktaeder både reknast og ikkje reknast som eit av desse.
Namnets opphav
[endre | endre wikiteksten]Dei arkimediske lekamane har namnet frå Arkimedes, som omtalte dei i eit mista verk. Gjennom renessansen gjekk kunstnarar og matematikarar gjennom reine former og gjenoppdaga alle desse formene. Denne leitinga blei fullført 1620 av Johannes Kepler,[A] som definerte prisma, antiprisma og stjerneformene kjent som Kepler-Poinsot-polyeder.
Tabell
[endre | endre wikiteksten]| Namn | Bilde | Lekam | Overflater | Kantar | Hjørne | |
|---|---|---|---|---|---|---|
| Avkutta tetraeder |  (animasjon) |
|
8 | 4 triangel 4 heksagonar |
18 | 12 |
| Kuboktaeder |  (animasjon) |
|
14 | 8 triangel 6 kvadrat |
24 | 12 |
| Avkutta kube |  (animasjon) |
|
14 | 8 triangel 6 oktogonar |
36 | 24 |
| Avskutta oktaeder |  (animasjon) |
|
14 | 6 kvadrat 8 heksagonar |
36 | 24 |
| Rombkuboktaeder |  (animasjon) |
|
26 | 8 triangel 18 kvadrat |
48 | 24 |
| Stor rombkuboktaeder |  (animasjon) |
|
26 | 12 kvadrat 8 heksagonar 6 oktogonar |
72 | 48 |
| Sløv kube |  (animasjon) |
|
38 | 32 triangel 6 kvadrat |
60 | 24 |
| Ikosidodekaeder | 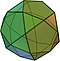Ikosidodekaeder (animasjon) |
|
32 | 20 triangel 12 pentagonar |
60 | 30 |
| Avkutta dodekaeder | 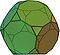Avstumpa dodekaeder (animasjon) |
|
32 | 20 triangel 12 dekagonar |
90 | 60 |
| Avkutta ikosaeder |  (animasjon) |
|
32 | 12 pentagonar 20 heksagonar |
90 | 60 |
| Rombikosidodekaeder | Rombikosidodekaeder (animasjon) |
|
62 | 20 triangel 30 kvadrat 12 pentagonar |
120 | 60 |
| Stor rombikosidodekaeder | Stor rombikosidodekaeder (animasjon) |
|
62 | 30 kvadrat 20 heksagonar 12 dekagonar |
180 | 120 |
| Sløv dodekaeder |  (animasjon) |
|
92 | 80 triangel 12 pentagonar |
150 | 60 |
Til slutt kan pseudorombkuboktaederet per definisjon både reknast og ikkje reknast som ein arkimedisk lekam:
| Namn | Bilde | Figur | Overflater | Kantar | Hjørne | |
|---|---|---|---|---|---|---|
| Pseudorombkuboktaeder | 
|
|
26 | 8 triangel 18 kvadrat |
48 | 24 |
Sjå òg
[endre | endre wikiteksten]Referansar
[endre | endre wikiteksten]- ↑ «Archimedian solid» (på engelsk). Wolfram MathWorld. Henta 19. august 2011.
Fotnotar
[endre | endre wikiteksten]- A Field J., Gjenoppdagelse av de arkimediske legemene: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler, Archive for History of Exact Sciences, 50, 1997, 227
 |