Arbeid i fysikk
Arbeid i fysikk eller mekanisk arbeid er ein skalar storleik som kan skildrast som produktet av krafta som påverkar ein lekam og strekninga lekamen vert forflytta i retninga til krafta. Om krafta verkar vinkelrett på forflyttinga, slik sentripetalkrafta gjer ved sirkelrørsle med konstant banefart, vert det ikkje utført noko arbeid. Omgrepet vart først gjeve namnet arbeid av den franske matematikaren Gaspard-Gustave Coriolis i 1826.[1][2]
Om ein løftar ein stein, utfører ein arbeid på steinen, og han får potensiell energi eller stillingsenergi. Om steinen fell utfører tyngdekrafta eit arbeid på steinen, og han får kinetisk energi eller rørsle energi. Ved friksjon går arbeidet over til auka rørsleenergi hos molekyla i stoffet, og den indre energien til lekamen aukar i form av auka temperatur i lekamen.
Arbeid vert målt i newtonmeter (Nm) = joule (J), eller i elektronvolt (eV). (1 eV=1,6 · 10-19 J). Joule er SI-eininga for arbeid.
Om ei konstant kraft med storleik F verkar på eit punkt som flyttar seg lengda d i retninga til krafta, så er arbeidet W gjort av denne krafta lik W=Fd. Til dømes om krafta er 10 newton og lengda er 2 meter, så er arbeidet lik 20 Nm = 20 J.
Den første termodynamikklova seier at når arbeid i termodynamikk vert utført på eit system (og ingen annan energi vert trekt frå på andre måtar), så endrar energitilstanden til systemet seg med same mengd som arbeidet ein utfører.
Einingar[endre | endre wikiteksten]
SI-eininga for arbeid er joule (J), som er definert som arbeidet gjort av ei kraft på ein newton over ein avstand på ein meter. Denne definisjonen er basert på Sadi Carnot sin definisjon frå 1824. Stundom vert den ekvivalente eininga newtonmeter (Nm) nytta for arbeid, men dette kan forvekslast med eininga newtonmeter for dreiemoment.
Einingar utanom SI-systemet er mellom anna erg, fot-pund, foot-poundal, liter-atmosfære, hestekraft-time, therm, BTU og kalori. Det er viktig å merke seg at varme og arbeid vert målt med å nytte dei same einingane.
Varmekonduksjon vert ikkje rekna som ei form for arbeid, sidan energien vert overført som vibrasjonar i atoma i staden for ei makroskopisk forflytting. Varmekonduksjon kan derimot utføre arbeid med å utvide gass ein ein sylinder, slik som i ein bilmotor.
Utrekning[endre | endre wikiteksten]
Om ei kraft F som er konstant med omsyn på tida, verkar på ein lekam forflytta langs vektoren d, så er arbeide utført på denne lekamen prikkproduktet av vektorane F og d:[3]
- (1)
der er vinkelen mellom krafta og forflyttingsvektoren.
Medan storleiken og retninga på krafta må vere konstant, kan vegen lekamen ta ha kva form som helst. Arbeidet som vert utført er uavhengig av vegen til sluttpunktet og vert berre avgjort av den totale forflyttingsvektoren . Eit vanleg døme er arbeidet gjort av tyngdekrafta - sjå figuren. Lekamen stig ned langs ei kurve, men arbeidet vert rekna ut frå , som gjev det vanlege resultatet .
Meir generelt, om krafta skapar (eller påverkar) rotasjon i lekamen, eller om lekamen ikkje er fast, så vert forflyttinga av punktet som krafta verkar på nyttast til å rekne ut arbeidet.
I situasjonar der krafta endrar seg over tid, gjeld ikkje lenger likning (1) generelt. Men det er mogeleg å dele rørsla inn i små steg, slik at krafta vert tilnærma konstant for kvart steg, og så uttrykke det totale arbeidet som somme av alle desse stega. Dette vil gje eit tilnærma resultat, som kan forbetrast med å vidare dele rørsla inn i mindre steg (numerisk integrasjon). Det eksakte resultatet får ein som den matematiske grensa til denne prosessen, og den generelle definisjonen nedanfor.
Den generelle definisjonen for mekanisk arbeid er gjeven av det følgjande linjeintegralet:
- (2)
der:
- er vegen eller kurva som punktet krafta verkar på flyttar seg langs;
- er kraftvektoren;
- er posisjonsvektoren; og
- er snøggleiken til punktet.
Uttrykket er eit unøyaktig differensial som tyder at utrekninga av er vegavhengig og ikkje kan differensierast til å gje .
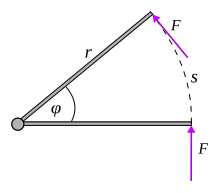
Likning (2) forklarar korleis ei kraft ulik null kan gjere null arbeid. Det enklaste tilfellet er når krafta alltid er vinkelrett til rørsleretninga, slik at integranden alltid er null. Dette skjer i sirkelrørsle. Sjølv om integranden stundom er ulik null, kan han likevel integrerast til null, om han stundom er negativ og stundom positiv.
Høvet for at ei kraft ulik null kan gjere null arbeid illustrerer skilnaden mellom arbeid og ein tilknytt storleik, impuls, som er den integrerte krafta over tid. Impuls måler endringa i rørslemengda til lekamen, ein vektorstorleik som er avhengig av retning, medan arbeid berre tar omsyn til storleiken av snøggleiken. Til dømes om ein lekam i sirkelrørsle gjer ei halv omdreiing, så gjer ikkje sentripetalkrafta noko arbeid, men overfører ein impuls ulik null.
Kjelder[endre | endre wikiteksten]
- Denne artikkelen bygger på «Work (physics)» frå Wikipedia på engelsk, den 26. mars 2012.
- Wikipedia på engelsk oppgav desse kjeldene:
- ↑ Jammer, Max (1957). Concepts of Force. Dover Publications, Inc. ISBN 0-486-40689-X.
- ↑ Sur une nouvelle dénomination et sur une nouvelle unité à introduire dans la dynamique, Académie des sciences, August 1826
- ↑ Resnick, Robert and Halliday, David (1966), Physics, Section 7-2 (Vol I and II, Combined edition), Wiley International Edition, Library of Congress Catalog Card No. 66-11527
Bakgrunnsstoff[endre | endre wikiteksten]
- Arbeid Arkivert 2010-12-14 ved Wayback Machine. – eit kapittel frå ei nettbaset lærebok (engelsk)













